NAME
tune_qnn_adaptive - Construct a multiplex with prescribed inter-layer correlations.
SYNOPSYS
tune_qnn_adaptive <degs1> <degs2> <mu> <eps> <beta> [RND|NAT|INV]
DESCRIPTION
This programs tunes the inter-layer degree correlation exponent μ. If we consider two layers of a multiplex, and we denote by k the degree of a node on the first layer and by q the degree of the same node on the second layers, the inter-layer degree correlation function is defined as:
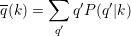 |
where q(k) is the average degree on layer 2 of nodes having degree k on layer 1.
The program assumes that we want to set the degree correlation function such that:
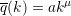 |
where the exponent of the power-law function is given by the user (it is indeed the parameter mu), and successively adjusts the pairing between nodes at the two layers in order to obtain a correlation function as close as possible to the desired one. The files degs1 and degs2 contain, respectively, the degrees of the nodes on the first layer and on the second layer.
The parameter eps is the accuracy of mu. For instance, if mu is set equal to -0.25 and eps is equal to 0.0001, the program stops when the configuration of node pairing corresponds to a value of the exponent μ which differs from -0.25 by less than 0.0001.
The parameter beta is the typical inverse temperature of simulated annealing.
If no other parameter is specified, or if the last parameter is RND, the program starts from a random pairing of nodes. If the last parameter is NAT then the program assumes that the initial pairing is the natural one, where the nodes have the same ID on both layers. Finally, if INV is specified, the initial pairing is the inverse pairing, i.e. the one where node 0 on layer 1 is paired with node N-1 on layer 2, and so on.
OUTPUT
The program prints on stdout a pairing, i.e. a list of lines in the format:
IDL1 IDL2
where IDL1 is the ID of the node on layer 1 and IDL2 is the corresponding ID of the same node on layer 2.
REFERENCE
V. Nicosia, V. Latora, “Measuring and modeling correlations in multiplex networks”, Phys. Rev. E 92, 032805 (2015).
Link to paper: http://journals.aps.org/pre/abstract/10.1103/PhysRevE.92.032805