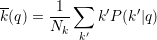
NAME
knn_q_from_degrees.py - compute the inter-layer degree-degree correlation function.
SYNOPSYS
knn_q_from_degrees.py <filein>
DESCRIPTION
Compute the inter-layer degree correlation functions for two layers of a multiplex, using the degrees of the nodes specified in the input file. The format of the input file is as follows
ki qi
where ki and qi are, respectively, the degree at layer 1 and the degree at layer 2 of node i.
If we consider two layers of a multiplex, and we denote by k the degree of a node on the first layer and by q the degree of the same node on the second layers, the inter-layer degree correlation function is defined as
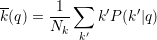 |
where P(k′|q) is the probability that a node with degree q on the second layer has degree equal to k′ on the first layer, and Nk is the number of nodes with degree k on the first layer. The quantity k(q) is the expected degree at layer 1 of node that have degree equal to q on layer 2. The dual quantity:
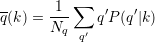 |
is the average degree on layer 2 of nodes having degree k on layer 1.
OUTPUT
The program prints on stdout a list of lines in the format:
k q(k)
where k is the degree on layer 1 and q(k) is the average degree on layer 2 of nodes having degree equal to k on layer 1.
The program also prints on stderr a list of lines in the format:
q k(q)
where q is the degree on layer 2 and k(q) is the average degree on layer 1 of nodes having degree equal to q on layer 2.
REFERENCE
V. Nicosia, V. Latora, “Measuring and modeling correlations in multiplex networks”, Phys. Rev. E 92, 032805 (2015).
Link to paper: http://journals.aps.org/pre/abstract/10.1103/PhysRevE.92.032805
V. Nicosia, G. Bianconi, V. Latora, M. Barthelemy, “Growing multiplex networks”, Phys. Rev. Lett. 111, 058701 (2013).
Link to paper: http://prl.aps.org/abstract/PRL/v111/i5/e058701
V. Nicosia, G. Bianconi, V. Latora, M. Barthelemy, “Non-linear growth and condensation in multiplex networks”, Phys. Rev. E 90, 042807 (2014).
Link to paper: http://journals.aps.org/pre/abstract/10.1103/PhysRevE.90.042807