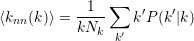
NAME
knn_q_from_layers.py - compute intra-layer and inter-layer degree-degree correlation coefficients.
SYNOPSYS
knn_q_from_layers.py <layer1> <layer2>
DESCRIPTION
Compute the intra-layer and the inter-layer degree correlation functions for two layers given as input. The intra-layer degree correlation function quantifies the presence of degree-degree correlations in a single layer network, and is defined as:
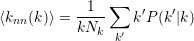 |
where P(k′|k) is the probability that a neighbour of a node with degree k has degree k′, and Nk is the number of nodes with degree k. The quantity ⟨knn(k)⟩ is the average degree of the neighbours of nodes having degree equal to k.
If we consider two layers of a multiplex, and we denote by k the degree of a node on the first layer and by q the degree of the same node on the second layers, the inter-layer degree correlation function is defined as
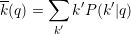 |
where P(k′|q) is the probability that a node with degree q on the second layer has degree equal to k′ on the first layer, and Nq is the number of nodes with degree q on the second layer. The quantity k(q) is the expected degree at layer 1 of node that have degree equal to q on layer 2. The dual quantity:
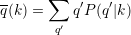 |
is the average degree on layer 2 of nodes having degree k on layer 1.
OUTPUT
The program creates two output files, respectively called
file1_file2_k1
and
file1_file2_k2
The first file contains a list of lines in the format:
k ⟨knn(k)⟩ σk q(k) σq
where k is the degree at first layer, ⟨knn(k)⟩ is the average degree of the neighbours at layer 1 of nodes having degree k at layer 1, σk is the standard deviation associated to ⟨knn(k)⟩, q(k) is the average degree at layer 2 of nodes having degree equal to k at layer 1, and σq is the standard deviation associated to q(k).
The second file contains a similar list of lines, in the format:
q ⟨qnn(q)⟩ σq k(q) σk
with obvious meaning.
REFERENCE
V. Nicosia, V. Latora, “Measuring and modeling correlations in multiplex networks”, Phys. Rev. E 92, 032805 (2015).
Link to paper: http://journals.aps.org/pre/abstract/10.1103/PhysRevE.92.032805
V. Nicosia, G. Bianconi, V. Latora, M. Barthelemy, “Growing multiplex networks”, Phys. Rev. Lett. 111, 058701 (2013).
Link to paper: http://prl.aps.org/abstract/PRL/v111/i5/e058701
V. Nicosia, G. Bianconi, V. Latora, M. Barthelemy, “Non-linear growth and condensation in multiplex networks”, Phys. Rev. E 90, 042807 (2014).
Link to paper: http://journals.aps.org/pre/abstract/10.1103/PhysRevE.90.042807